Ruikuan Liu, Tian Ma, Shouhong Wang and Jiayan Yang, Topological Phase Transition V: Interior Separations and Cyclone Formation Theory, 2017, Hal-01673496
This is the last one in this series of papers on topological phase transitions (TPTs); see I, II, III, and IV for details.
1. Interior separation of fluid flows is a common phenomenon in fluid dynamics, especially in geophysical fluid dynamics, such as the formation of hurricanes, typhoons and tornados, and gyres of oceanic flows. In general, the interior separation refers to sudden appearance of a vortex from the interior of a fluid flow.
It is clear that fluid interior separation is a typical TPT problem, similar to the TPT associated with boundary-layer separations. Also, mathematical, the geometric theory of incompressible flows developed by two of the authors offers the needed mathematical foundation for understanding interior separations, as well as for the quantum phase transitions of the Bose-Einstein condensates, superfluidity and superconductivity. For this geometric theory, see
[MW05] T. Ma & S. Wang, Geometric Theory of Incompressible Flows with Applications to Fluid Dynamics, AMS Mathematical Surveys and Monographs Series, vol. 119, 2005, 234 pp.
2. At the kinematic level, a structural bifurcation theorem theorem was proved in [MW05]. Basically, let 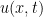 be a one-parameter family of 2D divergence-free vector fields with the first-order Taylor expansion with respect to
be a one-parameter family of 2D divergence-free vector fields with the first-order Taylor expansion with respect to  at
at 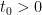 :
:

Let  be a degenerate singular point of
be a degenerate singular point of  , and the Jacobian
, and the Jacobian 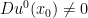 . Then, there are two orthogonal unit vectors
. Then, there are two orthogonal unit vectors  and
and 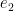 such that
such that

If  is an isolated singular point if
is an isolated singular point if  with
with 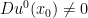 , and satisfies that
, and satisfies that

then 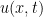 has an interior separation from
has an interior separation from  .
.
3. The above result is of kinematic in nature. We need to derive a separation equation, which connects the topological structure of the fluid flows to the solutions of the Navier-Stokes equations, which govern the the fluid motion.
For geophysical fluid phenomena such as hurricanes, typhoons, and tornados, the typical interior separation phenomena are caused by external wind-driven forces and by the non-homogenous temperature distributions. Therefore, the crucial factors for the formation of interior separations in the atmospheric and oceanic flows are
- the initial velocity field,
- the external force, and
- the temperature.
Hence the dynamical fluid model for interior separations has to incorporate properly the heat effect.
The Boussinesq equations are mainly for convective flows, and are not suitable for studying interior separations, associated in particular with the such geophysical processes as hurricanes, typhoons, and tornados.
For this purpose, we use the horizontal heat-driven fluid dynamical equations by Yang and Liu [18], which couple the Navier-Stokes equation and the heat diffusion equation with the following equations of state:

and

4. Consider the solution
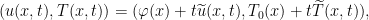
of the aforementioned fluid model with initial velocity  and initial temperature
and initial temperature 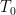 . One main result we obtain is the following interior separation equations:
. One main result we obtain is the following interior separation equations:


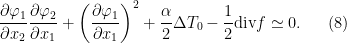
These separations include all physical information about the interior separations of the solution  for the system, in terms of the initial state
for the system, in terms of the initial state  and the external force
and the external force  .
.
5. Theoretical analysis and observations show that interior separation can only occur when
- one of you
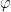 or
or  in (6) is U-shaped, which we call U-flow, and the other is either a U-flow or a flat flow; and
in (6) is U-shaped, which we call U-flow, and the other is either a U-flow or a flat flow; and
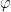 and
and  have reversed orientations.
have reversed orientations.
For the case where 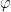 is a U-flow and
is a U-flow and  is a flat flow, the interior separation equations are expressed as:
is a flat flow, the interior separation equations are expressed as:


with the parameters satisfy
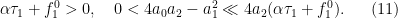
Here h.o.s.t referes to higher-order terms with small cofficients. Also we show that an interior separation takes place from  :
:
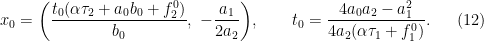
6. A typical development of a hurricane consists of several stages including an early tropical disturbance, a tropical depression, a tropical storm, and finally a hurricane stage.
Using the U-flow theory as described in Section 5 above, we derive the formation mechanism of tornados and hurricanes, providing precise conditions for their formation and explicit formulas on the time and location where tornados and hurricanes form:
Basically, we demonstrate that the early stage of a hurricane is through the horizontal interior flow separations, and we identify the physical conditions for the formation of the U-flow, corresponding to the tropical disturbance, and the temperature-driven counteracting force needed as the source for tropical depression. Basically, we demonstrate that the early stage of a hurricane is through the horizontal interior flow separations, and we identify the physical conditions for the formation of the U-flow, corresponding to the tropical disturbance, and the temperature-driven counteracting force needed as the source for tropical depression.
Ruikuan Liu, Tian Ma, Shouhong Wang and Jiayan Yang
